AND演算によるマスク
論理演算の用途には、 条件を結び付けることの他に、 データを部分的に変化させることがある。 これは、データの一部を覆い隠すような処理なので、マスク(mask) と呼ばれる。 AND 演算、 OR 演算、 XOR 演算によるマスクがよく使われる。 マスクでは、 データを2進数で表して、1ビット ごとに論理演算を行う。 1が真で、0が偽である。
最初は、 AND 演算によるマスクである。 例として、 01010110と00001111を AND演算してみよう。(下図) ここでは、 01010110 をデータと呼び、00001111をマスクパターンと呼ぶことにする。 演算結果は、 データの上位4ビットが0になり、下位4ビットは変化しない。 AND 演算によるマスクでは、マスクパターンの0に対応する部分が0にマスクされ、 1に対応する部分は変化しない。

AND演算によるマスク
| データ | マスク | 結果 | 説明 |
|---|---|---|---|
| 01010110 | 00001111 | 00000110 | マスクの0に対応するビットは0に、1に対応するビットはそのまま。➡ 上位4ビットが消え、下位4ビットが残る。 |
OR演算によるマスク
次は、 OR 演算によるマスクである。 例として、 01010110というデータと 00001111というマスクパターンをOR演算してみよう(下図)。 演算結果は、データの上位4ビットが変化せず、下位4ビットが1にマスクされた。 OR 演算によるマスクでは、マスクパターンの1に対応する部分が1にマスクされ、0に対応する部分が変化しない。

OR演算によるマスク
| データ | マスク | 結果 | 説明 |
|---|---|---|---|
| 01010110 | 00001111 | 01011111 | OR演算では、どちらかが1なら結果は1。➡ 下位4ビットがすべて1になり、上位4ビットはデータを維持。 |
XOR演算によるマスク
最後は、 XOR演算によるマスクである。 例として、 01010110というデータと 00001111というマスクパターンをXOR演算してみよう(下図)。 演算結果は、データの上位4ビットが変化せず、下位4ビットが反転(0が1になり、1が0になること)した。 XOR演算によるマスクでは、マスクパターンの1に対応する部分が反転し、0に対応する部分が変化しない。

. XOR演算によるマスク
| データ | マスク | 結果 | 説明 |
|---|---|---|---|
| 01010110 | 00001111 | 01011001 | XORは「異なると1、同じなら0」。➡ 下位4ビットが反転し、上位4ビットは変化しない。 |
すべての桁が1の11111111というマスクパターンで、 XOR 演算を行うとデータのすべての桁が反転する。 これは、 NOT演算を使っても実現できる。
複数桁の2進数を NOT演算すると、 すべての桁が反転するからである。
例えば、NOT(01010110) の演算結果は、10101001になる。
演算ごとのまとめ
| 演算種別 | 演算結果 | マスクの効果 |
|---|---|---|
| AND | 00000110 | マスクの0で対応ビットを強制的に0にする(消す) |
| OR | 01011111 | マスクの1で対応ビットを強制的に1にする(立てる) |
| XOR | 01011001 | マスクの1で対応ビットを反転させる(入れ替える) |
- AND → 特定ビットを消す
- OR → 特定ビットを立てる
- XOR → 特定ビットを反転する
上位ビットや下位ビットを得る
マスクの応用例として、データの上位ビットや下位ヒットを得る方法を紹介しよう。 例えば、8ビットの入れ物に格納された01010110というデータの下位4ビットの0110を得るには、どうしたらよいだろうか。コンピュータは、データの入れ物のサイズが決まっているので、8ビットの入れ物を分割して、4ビットだけ取り出すことはできない。
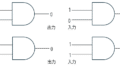
そこで、8ビットの入れ物の上位4ビットを0でマスクした00000110を、すなわち、01010110の下位4ビットを取り出したものとする。 上位4ビットを0でマスクし、下位4ビットを変化させないから、 01010110というデータと00001111というマスクパターンをAND演算すればよいことになる。(下図(1))
それでは、01010110というデータの上位4ビットの0101を得るには、 どうしたらよいだろう。この場合には、 まず、 11110000というマスクパターンとAND演算を行い、下位4ビットを0でマスクした01010000を得る。次に、 01010000を4ビット論理右シフトして、 00000101を得る。 01010000のままでは、0101を得たことにならない。 0101を右詰めにして00000101とすれば、 0101を得たことになる。(下図(2))

(参考)情報処理教科書 出るとこだけ!基本情報技術者[科目A][科目B]2025年版



コメント